Research - Applied Mathematics
Research Groups
The department's research efforts can be grouped into three broad areas, as delineated below. These areas have considerable overlap and several faculty consider themselves associated with more than one group. Beyond the areas listed below, a number of researchers from the department have major interdisciplinary connections to researchers from other departments across the campus. Indeed there are very prominent collaborations with the departments of Computer Science, Defense Analysis, Electrical and Computer Engineering, Mechanical and Aerospace Engineering, Meteorology, Oceanography, Operations Research, and Physics.
Applied Analysis
Applied analysis is concerned with the interface between fundamental mathematical structures which rely on continuity and their use in the physical and social sciences. This research group has diverse interests that include asymptotic analysis, control theory, mechanics (fluid and orbital), and game theory. There are significant overlaps with the research group in Scientific Computing.
Faculty Members in the Applied Analysis Group
Chris Frenzen
Wei Kang
Art Krener
Clyde Scandrett
Previous Postdoctoral Members in the Applied Analysis Group
Caesar Aguilar (now a professor at SUNY Geneseo)
Thomas Hunt (now at Hurricane Electric)
View slides from the Computational Issues in Nonlinear Control conference.
Discrete Mathematics
Discrete mathematics, sometimes called finite mathematics, is the study of mathematical structures that are fundamentally discrete, in the sense of not supporting or requiring the notion of continuity. Discrete mathematics is extensively used in a variety of critical applications such as cryptography, coding theory, combinatorics, network analysis, and search algorithms for the internet.
Faculty Members in the Discrete Mathematics Group
Ralucca Gera
Thor Martinesen
Pante Stanica
Visitors in the Discrete Mathematics Group
Tron Omland (Norwegian National Security Agency)
Scientific Computing
Scientific Computing is the study of theories, computational methods, numerical algorithms, and other tools required to practically solve mathematical models of problems from science and engineering in a robust, accurate, and efficient manner. The primary goal is the development of novel techniques and approaches to approximation and efficient computation that are at the heart of modern science. This research group is primarily focused on the numerical solution of partial and ordinary differential equations, numerical linear algebra, and approximation theory. There are significant overlaps with the research group in Applied Analysis.
Current projects being worked on by the group include earthquake modeling (funded by NSF), the construction of scalable numerical methods for climate modeling (funded by NSF), the development of new governing equations and numerical methods for space weather (funded by DARPA), and the development of sub grid-scale processes for better understanding extreme weather events such as tropical cyclones using super-parameterization and scientific machine learning methods (funded by ONR).
Faculty Members in the Scientific Computing Group
Anthony Austin
Carlos Borges
Frank Giraldo
Lucas Wilcox
Hong Zhou
Current Postdoctoral Members in the Scientific Computing Group
Kiran Jadhav (from IIT, Mumbai, India)
Soonpil Kang (from University of Illinois, Urbana-Champaign)
Previous Postdoctoral Members in the Scientific Computing Group
Daniel Abdi (now a scientist at ESRL/NOAA)
Felipe Augusto de Braganca Alves (now at the University of Sao Paolo)
Sergey Charnyi (now at Siemens)
Shiva Gopalakrishnan (now a professor at IIT Mumbai)
Thomas Gibson (now a scientist at AMD)
James Kelly (now a scientist at NRL DC)
Michal Kopera (now a professor at Boise St.)
Simone Marras (now a professor at NJIT)
Andreas Mueller (now a scientist at ECMWF)
Sohail Reddy (now at scientist at LLNL/DOE)
Maciek Waruszewski (now a postdoc at SNL/DOE)
Research Collaboration
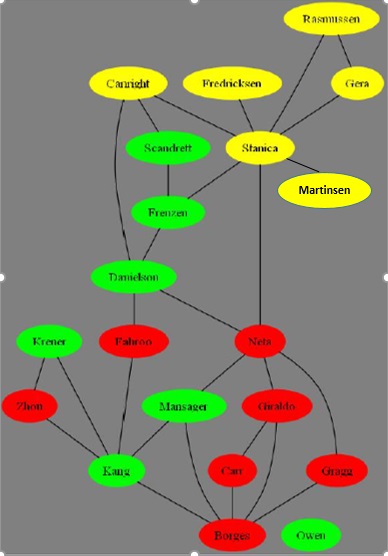
There is a high degree of collaboration within the department which can be seen in the graph on the right that shows links between all of our faculty who have published jointly.
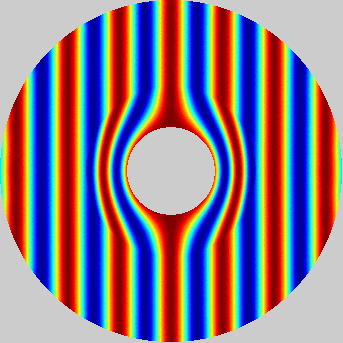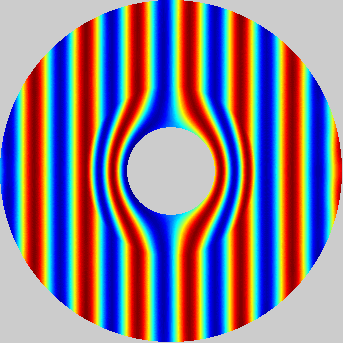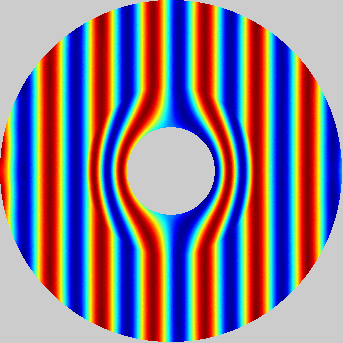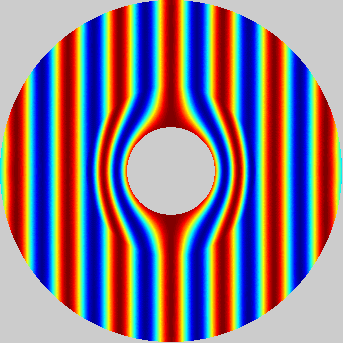
An example of transformational acoustics, demonstrating near field bending of an incoming plane wave about an acoustically hard sphere at a ka value of approximately 5.2. Principal Investigator: Clyde Scandrett
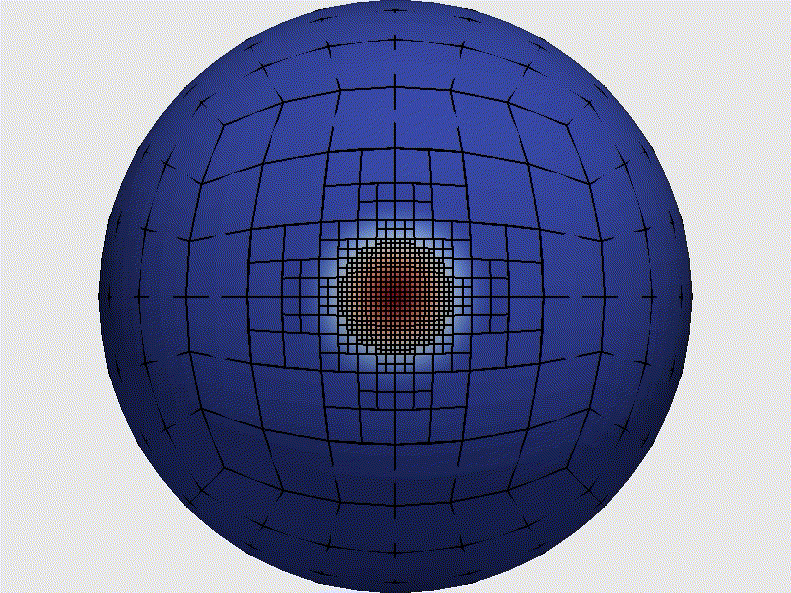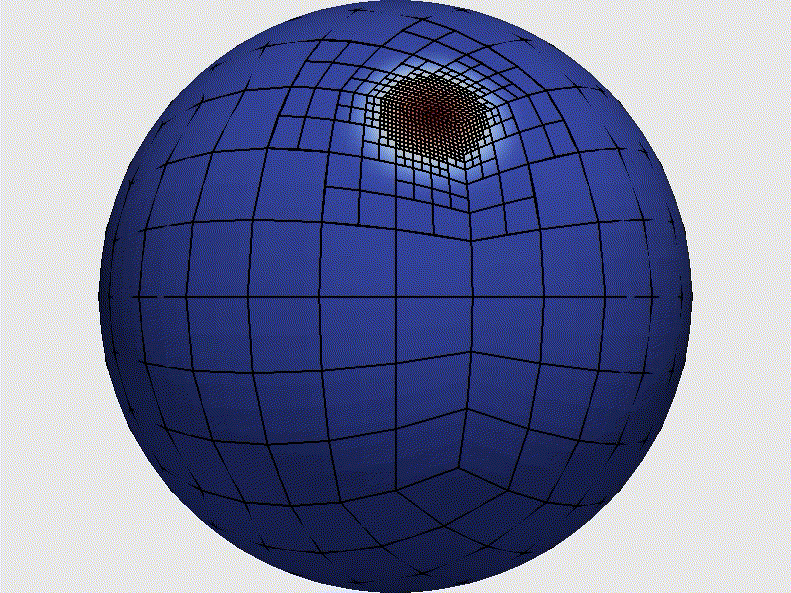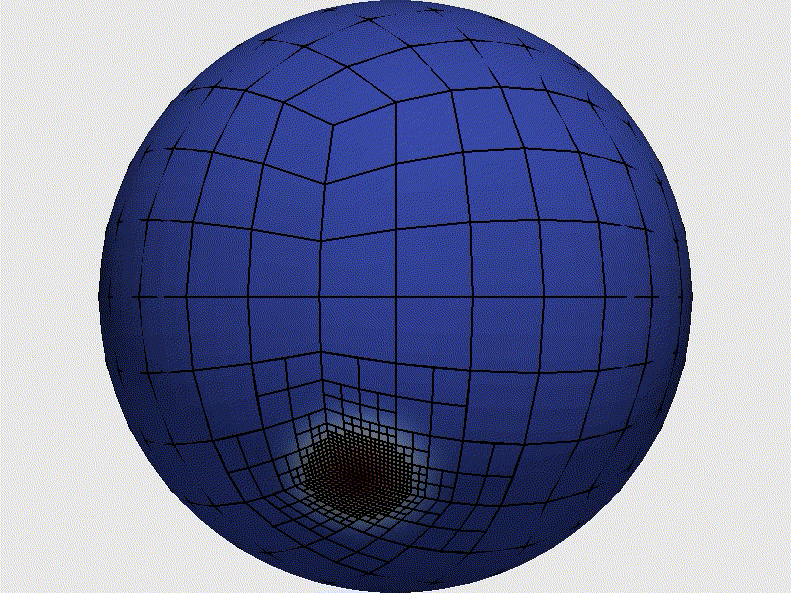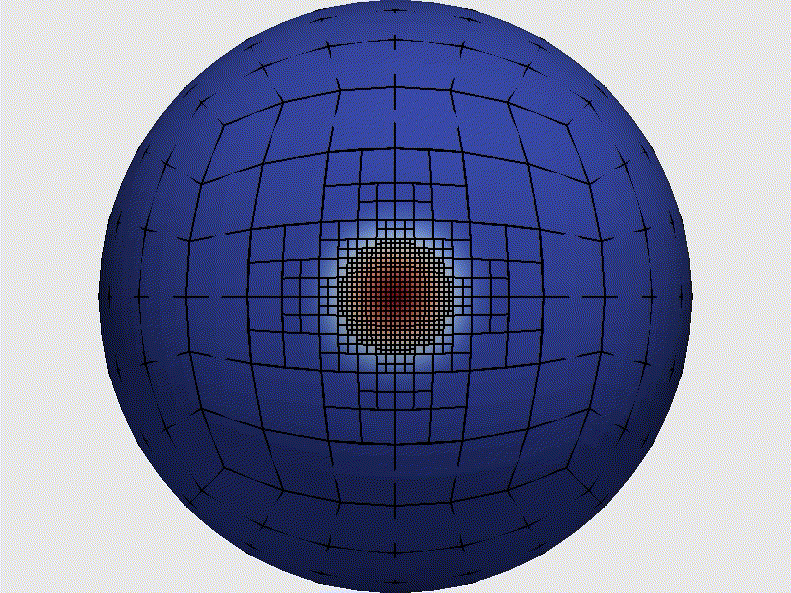
Adaptive Mesh Refinement (AMR) tracking a tracer across the surface of the Earth (imagine a hurricane). Former NRC postdoc Michal Kopera (now Assoc. Prof. at Boise State), simulated this test using the NUMA model that tracks the tracer over 12 days. Principal Investigator: Frank Giraldo
A few examples of Generalized Petersen graphs of skip 2, whose spectrum is now known. Principal Investigators: Ralucca Gera & Pante Stanica